Lei de Hess
A Lei de
Hess constitui uma "ferramenta" poderosa para o cálculo da variação de
entalpia de reações que não podem ser determinadas experimentalmente.
O processo
para a resolução consiste em trabalhar convenientemente com as equações
fornecidas de modo que, de sua soma algébrica, resulta na equação
principal, possibilitando o cálculo do 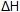 .
.
De acordo com o Princípio da Conservação da Energia, esta não pode ser criada, nem destruída, apenas transformada.
Suponha as seguintes transformações:

A transformação do reagente A em produto B pode ocorrer por dois caminhos:
- direto, com variação de entalpia
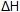 1,
1, - em etapas, do reagente A para o intermediário C, com variação de entalpia
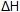 2, e daí para o produto B, com calor de reação
2, e daí para o produto B, com calor de reação 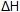 3.
3.
Como a energia não pode ser criada nem destruída, então: 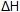 1 =
1 = 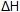 2 +
2 + 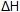 3.
3.
Caso esta igualdade não se verifique, teríamos perdido ou ganho energia, contrariando o Princípio da Conservação.
Em decorrência do Princípio da Conservação de Energia, a Lei de Hess diz que:
"A variação de entalpia de uma reação química depende apenas dos estados inicial e final do sistema, não importando etapas intermediárias pelas quais a transformação química passou".
Em outras palavras, se uma transformação química ocorre em várias etapas, o 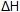 da reação será igual à soma das variações de entalpia das diversas etapas.
da reação será igual à soma das variações de entalpia das diversas etapas.
Como conseqüência podemos somar duas ou mais equações termoquímicas e o 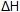 da equação resultante será igual à soma dos
da equação resultante será igual à soma dos 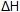 das equações adicionadas.
das equações adicionadas.
A Lei de
Hess constitui uma "ferramenta" poderosa para o cálculo da variação de
entalpia de reações que não podem ser determinadas experimentalmente.
O processo
para a resolução consiste em trabalhar convenientemente com as equações
fornecidas de modo que, de sua soma algébrica, resulta na equação
principal, possibilitando o cálculo do 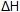 .
.
Além disso, devemos lembrar que na Lei de Hess:
- invertendo uma equação, o
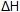 muda de sinal,
muda de sinal,
- multiplicando os coeficientes de uma equação por um número, o
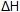 também fica multiplicado por esse número.
também fica multiplicado por esse número.
Exemplo:
O calor de formação do metano, CH4, não pode ser determinado por
medidas calorimétricas pois a reação é lenta e apresenta reações
secundárias.
A partir das seguintes equações
I. C(grafite) + O2(g) ⇔ CO2(g)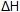 = - 94,05 kcal
= - 94,05 kcal
I. C(grafite) + O2(g) ⇔ CO2(g)
II. H2(g) + ½ O2(g) ⇔H2O(l) 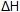 = - 68,32 kcal
= - 68,32 kcal
III. CH4(g) + 2 O2(g) ⇔ CO2(g) + 2 H2O(l) 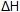 = - 212,87 kcal
= - 212,87 kcal
pode-se determinar a variação da entalpia da reação de formação do metano:
C(grafite) + 2 H2(g) ⇔CH4(g) 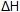 = ?
= ?
As seguintes operações devem ser feitas:
- manter a equação I
- multiplicar a equação II por 2
- inverter a equação III
Assim,
C(grafite) + O2(g) ⇔ CO2(g) 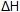 = - 94,05 kcal
= - 94,05 kcal
H2(g) + ½ O2(g) ⇔ H2O(l) 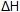 = 2.(- 68,32) kcal
= 2.(- 68,32) kcal
CO2(g) + 2 H2O(l) ⇔CH4(g) + 2 O2(g) 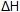 = + 212,87 kcal
= + 212,87 kcal
__________________________________________________
C(grafite) + 2 H2(g) ⇔ CH4(g)
Exercícios ( Respostas no final da página)
01.
Com o objetivo de solucionar o problema da grande demanda de energia
proveniente de fontes energéticas não-renováveis, uma das alternativas
propostas é o uso da biomassa, matéria orgânica que quando fermenta,
produz biogás, cujo principal componente é o metano, utilizado em usinas
termelétricas, gerando eletricidade, a partir da energia térmica
liberada na sua combustão.
O calor envolvido, em kJ, na combustão de 256 g do principal componente do biogás é, aproximadamente,
Dados:
C(graf) + 2H2(g) → CH4(g) ∆H = -74,4 kJ/mol
H2(g) + ½ O2(g) → H2O(g) ∆H = -242,0 kJ/mol
C(graf) + O2(g) → CO2(g) ∆H = -393,5 kJ/mol
(A) –801,0.
(B) +1.606,0.
(C) –6.425,0.
(D) +8.120,0.
(E) –13.010,0.
02. Dadas as equações termoquímicas:
C(graf) + O2(g) → CO2(g) ∆H = -393 kJ/mol
H2(g) + ½ O2(g) → H2O(l) ∆H = -286,0 kJ/mol
2 C(graf) + 2 H2(g) + O2(g) → CH3COOH(l) ∆H = -484,0 kJ
A entalpia-padrão de combustão de um mol de ácido acético é
(A) + 874 kJ.
(B) +195 kJ.
(C) –195 kJ.
(D) –874 kJ.
(E) –1163 kJ.
03. Observe os dados a seguir:
2 Mg(s) + O2(g) → 2 MgO(s) ∆H = -1203,6 kJ
Mg(OH)2(s) → MgO(s) + H2O(l) ∆H = +37,1 kJ
2 H2(g) + O2(g) → 2 H2O(l) ∆H = -571,7 kJ
Baseando-se no exposto acima, a entalpia padrão do Mg(OH)2(s), a 25ºC e 1 atm, é, aproximadamente,
(A) +850,5 kJ.
(B) +37,1 kJ.
(C) -37,1 kJ.
(D) -887,6 kJ.
(E) -924,7 kJ.
04. Para calcular a variação de entalpia da reação (∆HR), representada por:
Hidroquinona (C6H5O2) + H2O2 → quinona (C6H4O2) + 2 H2O(l)
foram utilizados os seguintes dados:
– combustão do H2(g) com O2(g)
produzindo H2O(l) ∆H1= –286 kJ/mol de H2O
– decomposição do H2O2, em meio aquoso,
produzindo H2O(l) e O2(g)… ∆H2= –95 kJ/mol de H2O
– hidrogenação (H2) da quinona produzindo hidroquinona ∆H3= –177 kJ/mol
O valor calculado de(∆HR), em kJ/mol é da ordem de
(A) +200
(B) +100
(C) –100
(D) –150
(E) –200
05. Quando o óxido de magnésio está na presença de uma atmosfera de gás carbônico, este é convertido a carbonato de magnésio.
São dadas as entalpias-padrão de formação:
Mg(s) + ½ O2(g) → MgO(s) ∆H = -602 kJ/mol
C(graf) + O2(g) → CO2(g) ∆H = -394 kJ/mol
Mg(s) + C(graf) + 3/2 O2(g) → MgCO3(s) ∆H = -1096 kJ/mol
A formação de um mol de carbonato de magnésio, a partir do óxido de magnésio e gás carbônico, é uma reação
(A) endotérmica, com valor absoluto de entalpia de 100 kJ.
(B) exotérmica, com valor absoluto de entalpia de 100 kJ.
(C) endotérmica, com valor absoluto de entalpia de 888 kJ.
(D) exotérmica, com valor absoluto de entalpia de 888 kJ.
(E) endotérmica, com valor absoluto de entalpia de 1 304 kJ.
06 - (Unimontes MG/2008)- A equação a seguir mostra a isomerização dos ácidos maléico e fumárico:
O
ácido maléico é o isômero cis e o ácido fumárico é o trans. As
entalpias de combustão dos ácidos maléico e fumárico são,
respectivamente, –1355,2 e –1334,7. Baseando-se nesses dados, a entalpia
de isomerização cis-trans, em kJ mol–1, representada na equação acima, é
(A) +20,5.
(B) –20,5.
(C) +1334,7.
(D) –1334,7.
(E) +1121,5.
07.
A respiração celular é um processo vital e ocorre por meio de reações
químicas. Um exemplo pode ser a conversão da glicose em ácido pirúvico
por meio da reação:
C6H12O6(S) + O2(g) → 2 C3H4O3(s) + 2 H2O(l)
glicose ácido pirúvico
Considere as reações a 25 ºC e 1 atm:
C6H12O6(s) + 6 O2(g) → 6 CO2(g) + 6 H2O(l) ∆H = -2808 kJ/mol
C3H4O3(s) + 5/2 O2(g) → 3 CO2(g) + 2 H2O(l) ∆H = -1158 kJ/mol
Pode-se então afirmar que, na formação do ácido pirúvico a partir de 1 mol de glicose, há
(A) liberação de 492 kJ de energia.
(B) absorção de 492 kJ de energia.
(C) liberação de 1650 kJ de energia.
(D) absorção de 1650 kJ de energia.
(E) liberação de 5124 kJ de energia.
08.
Durante a produção industrial do ácido sulfúrico são necessárias as
seguintes etapas intermediárias: combustão do enxofre e oxidação do
dióxido de enxofre.
2 S(s) + 3 O2(g) → 2 SO3(g) ∆H = -791,44 kJ
S(s) + O2(g) → SO2(g) ∆H = -296,83 kJ
Determine a entalpia padrão de formação do trióxido de enxofre de acordo com a reação abaixo:
2 SO2(g) + O2(g) → 2 SO3(g)
(A) – 197,78 kJ
(B) – 1088,27 kJ
(C) + 197,78 kJ
(D) – 494,61 kJ
(E) + 1088,27 kJ
09. A gaseificação da biomassa pode produzir uma mistura gasosa que, entre outras substâncias, contém CO e H2,
mistura esta conhecida como gás de síntese. A partir deste gás de
síntese, pode-se obter o dimetil – éter, outro combustível alternativo,
com potencial para substituir combustíveis derivados do petróleo. Este
processo é complexo e envolve uma série de reações, como as
representadas pelas seguintes equações termoquímicas:
CO + H2O → CO2 + H2 ∆H = -40,9 kJ
CO2 + 3 H2 → CH3OH + H2O ∆H = -56,3 kJ
2 CH3OH → CH3OCH3 + H2O ∆H = -21,3 kJ
Resultados experimentais mostram que, para cada mol de dimetil – éter produzido, se forma também um mol de CO2. Assim, a quantidade de calor, em kJ, envolvida na produção de 1 mol de dimetil – éter + 1 mol de CO2 a partir do gás de síntese, é
(A) – 21,3
(B) – 118,5
(C) – 256,6
(D) + 75,9
(E) + 214,0
10. Considere as seguintes equações termoquímicas:
N2(g) + 3 O2(g) + H2(g) → 2 HNO3(aq) ∆H = -415 kJ
2 H2(g) + O2(g) → 2 H2O(l) ∆H = -572 kJ
N2O5(g) + H2O(l) → 2 HNO3(aq) ∆H = -140 kJ
A entalpia de formação do pentóxido de nitrogênio, em kJ/mol, é igual a
(A) –847.
(B) –11,0.
(C) +11,0.
(D) +22,0.
(E) +847.
GABARITO: 1)E 2)D 3) 4)E 5)B 6)B 7)A 8)A 9)C 10)C

como se resolve a questão 8?
ResponderExcluir